Learn the fundamentals of Kirchhoffs Voltage Law (KVL), its applications in DC circuits, and how to effectively apply it in real-world scenarios. This in-depth guide will take you through the principles of KVL, step-by-step examples, and useful tips for mastering this essential law in circuit analysis.
Introduction to Kirchhoff’s Voltage Law
Kirchhoff’s Voltage Law (KVL) is a fundamental law in electrical engineering that states the algebraic sum of the potential differences (voltages) in any closed loop or mesh in a network is always equal to zero. This principle is based on the conservation of energy in electrical circuits and is essential for analyzing and solving complex circuits.
Understanding the Basics of DC Circuits
Before diving into KVL, it’s crucial to understand the basics of direct current (DC) circuits. DC circuits consist of voltage sources, such as batteries, and various passive components like resistors, capacitors, and inductors. In a DC circuit, current flows in one direction, making it easier to analyze and apply KVL.
Key Components in DC Circuits
- Voltage Source: A device that provides a constant potential difference (voltage) across its terminals.
- Resistor: A passive component that opposes the flow of current, producing a voltage drop proportional to the current passing through it.
- Capacitor: A passive component that stores electrical energy in an electric field and opposes the change in voltage.
- Inductor: A passive component that stores electrical energy in a magnetic field and opposes the change in current.
The Role of Loop and Mesh Analysis
Loop and mesh analysis are essential techniques for applying KVL to complex circuits. A loop is a closed conducting path in a circuit, while a mesh is the simplest form of a loop, containing no other loops within it. In loop analysis, KVL is applied to every loop in the circuit, while in mesh analysis, KVL is applied to every mesh.
Kirchhoff’s Voltage Law Formula
Kirchhoff’s Voltage Law (KVL) is a fundamental principle in electrical circuit analysis that states that the algebraic sum of all voltages around any closed loop in a circuit is zero. In mathematical terms, it can be expressed as:
ΣV = 0
where ΣV is the sum of all voltage drops across all the circuit components around a closed loop and is equal to zero.
This equation can be illustrated with a simple circuit diagram as shown below:

where Vs is the voltage source, R1 and R2 are resistors.
According to KVL, the sum of all voltage drops around the loop in the above circuit must be equal to zero. Therefore, we can write:
Vs – V1 – V2 = 0
where V1 is the voltage drop across R1 and V2 is the voltage drop across R2.
Since the current flows through both resistors in series, the current through each resistor will be the same, i.e., I = I1 = I2.
Using Ohm’s law, we can write:
V1 = IR1 and V2 = IR2
Substituting these values into the KVL equation, we get:
Vs – IR1 – IR2 = 0
Rearranging the terms, we get:
Vs = IR1 + IR2
This equation shows that the total voltage supplied by the source is equal to the sum of the voltage drops across the two resistors. This is consistent with the principle of conservation of energy, which states that the total energy supplied by the source must be equal to the total energy consumed by the circuit components.
In summary, Kirchhoff’s Voltage Law is an important tool in circuit analysis that can be used to determine the voltage drops across various circuit components. By applying this principle to different loops in a circuit, the values of unknown voltages and currents can be calculated, allowing the performance and behavior of the circuit to be predicted and analyzed.
The Mathematical Equation
The KVL equation can be written as:
Sum of Voltage Gains – Sum of Voltage Losses = 0
or, more specifically:
Sum of V_source – Sum of (I * R) = 0
In this equation:
- V_source represents the voltage gain from a voltage source, such as a battery or power supply.
- I is the current flowing through a resistor in the loop.
- R is the resistance of the resistor.
Breaking Down the Equation
Let’s break down the equation further to understand how it works in a circuit:
- Voltage Gains (V_source): These are the voltage increases in the circuit, which are typically provided by voltage sources like batteries or power supplies. Each voltage source contributes to the total voltage gain in a closed loop.
- Voltage Losses (I * R): These are the voltage decreases in the circuit, which occur when the current flows through resistors or other passive components. The voltage drop across a resistor is calculated by multiplying the current (I) flowing through the resistor by the resistor’s resistance (R).
By stating that the sum of voltage gains minus the sum of voltage losses must equal zero, KVL ensures that the conservation of energy holds true in a closed loop.
Step-by-Step Guide to Applying Kirchhoff’s Voltage Law
Follow these steps to apply KVL in DC circuits:
- Identify loops or meshes: Examine the circuit and identify all the loops or meshes.
- Assign current directions: Arbitrarily assign a current direction (clockwise or counterclockwise) for each loop or mesh.
- Apply KVL to each loop or mesh: For each loop or mesh, write a KVL equation that represents the sum of the voltages in the loop or mesh, ensuring that the voltage signs correspond to the assigned current directions.
- Solve the system of equations: Use algebraic methods, such as substitution, elimination, or matrix techniques, to solve the system of KVL equations and determine the unknown currents in each loop or mesh.
- Calculate other circuit parameters: Once you have the currents, use Ohm’s Law and other circuit relationships to determine additional circuit parameters, such as voltage drops across components and total power dissipation.
Kirchhoff’s Voltage Law in Complex Circuits
When working with complex circuits that contain multiple loops and meshes, KVL can still be effectively applied using the loop or mesh analysis techniques. For circuits with multiple voltage sources and resistors, follow these guidelines:
- Simplify the circuit: If possible, reduce the complexity of the circuit by combining series and parallel resistors or voltage sources.
- Apply loop or mesh analysis: As discussed earlier, identify loops or meshes and apply KVL to each, creating a system of equations.
- Solve the system of equations: Use appropriate algebraic methods to solve the equations and find the unknown currents.
- Determine additional circuit parameters: Calculate voltage drops, power dissipation, and other relevant parameters using the found currents.
KVL in Parallel Circuits
In a circuit containing parallel loops, KVL can be applied to each loop independently. When analyzing parallel loops, it is essential to remember that the voltage across elements connected in parallel is the same for each loop. By applying KVL to each loop and setting up a system of equations, it is possible to determine the unknown voltages and currents in the circuit.
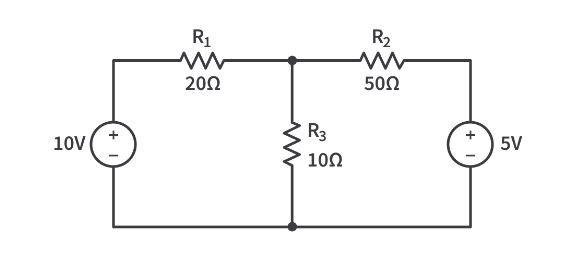
To apply Kirchhoff’s Voltage Law in parallel loops, follow these steps:
- Identify loops: Determine the number of independent loops in the circuit.
- Assign loop currents: Assign a current variable to each loop, typically following a clockwise direction.
- Apply KVL to each loop: Write an equation for each loop, summing the voltage drops and rises. Ensure that the algebraic sum of the voltages in each loop equals zero.
- Solve the system of equations: Use mathematical techniques, such as substitution or matrix methods, to solve the system of equations and find the unknown currents and voltages.
Example Application
Consider a circuit with two resistors (R1 and R2) connected in parallel across a voltage source (V). To apply KVL to this circuit, you can create two independent loops:
- Loop 1: The voltage source and resistor R1.
- Loop 2: The voltage source and resistor R2.
Applying KVL to each loop, you will have two equations:
- Loop 1: V – I1 * R1 = 0
- Loop 2: V – I2 * R2 = 0
These equations can be solved for the loop currents (I1 and I2), allowing you to analyze the circuit behavior.
Real-World Applications and Practical Tips
Kirchhoff’s Voltage Law is widely used in various fields, including electronics, power systems, and telecommunications. Some real-world applications include:
- Circuit troubleshooting and fault detection: KVL can be used to verify the integrity of circuits and identify faults, such as short circuits or open circuits.
- Circuit design and optimization: Engineers use KVL to design and optimize circuits, ensuring that components are correctly sized and power losses are minimized.
Here are some practical tips for mastering KVL:
- Familiarize yourself with the basics of DC circuits, including voltage sources, resistors, capacitors, and inductors.
- Practice applying KVL to simple circuits, gradually increasing the complexity.
- Pay attention to the polarity of voltage sources and the direction of currents when writing KVL equations.
- Use a systematic approach when analyzing complex circuits, simplifying where possible and keeping track of all variables.
Kirchhoff’s Voltage Law is a vital tool for understanding and analyzing DC circuits. By mastering the principles of KVL, loop and mesh analysis, and following a step-by-step approach to solving circuit problems, you can become proficient in this essential aspect of electrical engineering. With practice and application, you’ll be able to tackle complex circuits and real-world problems, ensuring that your knowledge of KVL remains an invaluable skill in your engineering toolkit.
(Video) KVL Explained
PDFs and Technicals
Useful Resources
Mastering Basic Electronic Circuit Schematic Symbols
Top 5 Multimeters for Electricians: Pros and Cons (2023)
Three Phase Motors Explained in 10 Minutes
How to: Wiring a Three Way Switch Using NM Cable
Wiring a 4 Way Switch: Step by Step Guide
FAQ
What is Kirchhoff’s law of voltage?
Kirchhoff’s law of voltage, also known as Kirchhoff’s Voltage Law (KVL), states that the sum of the voltages around any closed loop in an electrical circuit is equal to zero. In other words, the total voltage supplied in a loop is equal to the total voltage consumed by the components within that loop. KVL is based on the principle of energy conservation and is essential for analyzing and designing electrical circuits.
What is Kirchhoff’s Law used for?
Kirchhoff’s Laws, including Kirchhoff’s Current Law (KCL) and Kirchhoff’s Voltage Law (KVL), are fundamental tools for analyzing electrical circuits. They are used to:
1. Calculate unknown voltages, currents, or component values in a circuit.
2. Simplify complex circuits for easier analysis.
3. Verify the consistency of voltage and current distributions within a circuit.
4. Identify potential faults or discrepancies in circuit designs.
5. Develop a deeper understanding of circuit behavior and performance.
Why does Kirchhoff’s voltage law work?
Kirchhoff’s Voltage Law works due to the conservation of energy principle. In an electrical circuit, energy is supplied by voltage sources (e.g., batteries, generators) and consumed by components (e.g., resistors, capacitors, inductors). KVL ensures that the energy provided by voltage sources is equal to the energy consumed by the components in any closed loop. Since no energy is lost within an ideal closed loop, the sum of the voltage drops and rises must equal zero, as described by KVL.
What is the difference between Kirchhoff’s current law and Kirchhoff’s voltage law?
Kirchhoff’s Current Law (KCL) and Kirchhoff’s Voltage Law (KVL) are both fundamental principles used in circuit analysis, but they address different aspects of electrical circuits:
Kirchhoff’s Current Law (KCL): KCL states that the sum of the currents entering a junction in a circuit is equal to the sum of the currents leaving that junction. In other words, the total current is conserved at any point in a circuit. KCL is based on the principle of charge conservation and is mainly applied to analyze parallel circuits or node voltages.
Kirchhoff’s Voltage Law (KVL): KVL states that the sum of the voltages around any closed loop in a circuit is equal to zero. This law is based on the principle of energy conservation and is primarily used to analyze series and complex circuits, as well as verify voltage consistency in parallel circuits.